城市街道视域景观特征与邻里尺度的特征效应

摘要：本文探讨了城市街道视域景观特征与邻里尺度的特征效应，详细介绍了基于视域景观指数（如GVI、SVF等）的计算流程。通过引入邻元数作为空间尺度配置模式，利用层次聚类与方差分析法，研究了不同邻里尺度下最优簇数的变化规律、景观指数的贡献度差异以及特征聚类的空间分布。结果表明，视域景观特征具有显著的尺度依存性，随着邻里尺度增加，特征集聚效应逐渐减弱，且主导特征由局部性向区域性转变。

关键词：城市街道；视域景观指数；邻里尺度；特征效应；层次聚类；贡献度分析

1 计算流程说明

计算流程分为4部分。

1）选择视域景观指数，包括GVI、SVF、GVP、ED、PARA、SHAPE、FRAC、CRI和KPSF，其中KPSF包括区间（0，10]、（10，20]、（20，30]和（30，40]。

2）确定以邻元数为空间尺度配置模式，即各个采样点相邻采样点的个数。配置区间为20个连续序列的邻元数：5~50m，每5m一个间隔；50~150m，每10m一个间隔。该参数由层次聚类AgglomerativeClustering方法的输入参数connectivity（连接矩阵）控制，并由kneighbors_graph方法输入邻元数计算。

3）计算各个邻里尺度层次聚类最优簇数，由KElbowVisualizer方法计算，即计算每个点到其所属聚类中心的平方距离之和，曲线拐点即为最优的簇数选择。聚类将所有采样点按视域景观指数划分为多个簇（组），每簇内的采样点由视域景观指数赋予相似的特征，增加簇间而缩小簇内的特征异质性，就是寻找最优簇数的过程；

4）由最优簇数聚类指数获得各邻里尺度特征分布，并计算指数（特征）贡献度，由SelectKBest方法的方差分析法（analysis of variance, ANOVA）为指数打分计算（配置参数为f_classif），反映聚类簇标签与特征之间线性依赖程度，较高的分值表明该指数对聚类结果有较大影响，为所选指数中对城市街道视域景观特征分布有主要影响的因子。

2.2.1 不同邻里尺度最优簇数

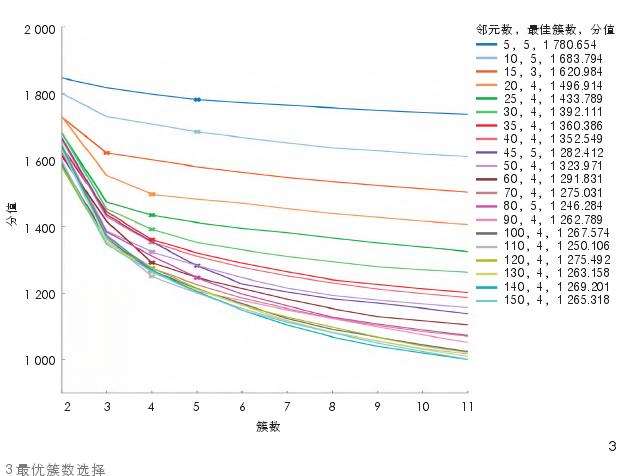
从最终计算结果（图3）可以观察到，20个连续邻里尺度的最优簇数集中于4，其次为5，只有当邻元数为15时，簇数为3。同时可以观察到，当邻元数增加，邻里尺度增大时，不同邻里尺度聚类的测量分值（配置参数为distortion，即计算从每个点到其指定中心的平方距离之和）拉开的距离开始减小。这表明视域景观指数随邻里尺度的增加，在相同簇数下，较高的邻元数趋向于较低的分值，表现为簇间的异质性相对不明显，簇内的异质性有所增加，对特征集聚的效应有所减弱。

2.2.2 不同邻里尺度景观指数贡献度

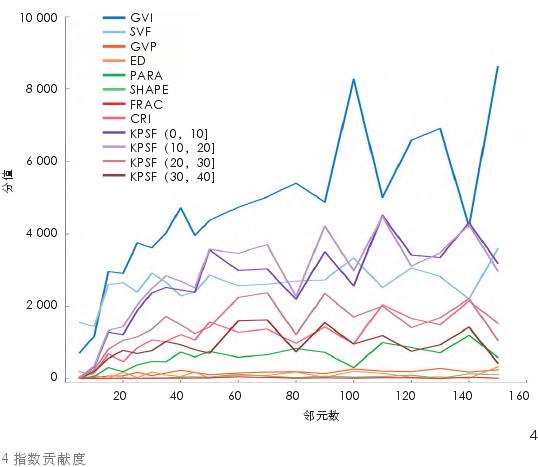
从最终计算结果（图4）可以观察到：不同邻里尺度下GVI对聚类特征的贡献度基本占绝对优势；其次为KPSF（10，20]、KPSF（0，10]和SVF；再者为CRI、KPSF（20，30]、PARA、KPSF（30，40]；对聚类特征贡献度最小的是ED、GVP、SHAPE、FRAC。其中当邻元数小于40时，GVI和SVF占主导；邻元数大于等于40时，主要以GVI和KPSF（10，20]、KPSF（0，10]占主导。

贡献度的分值变化同最优簇数选择分值变化均具有邻里尺度效应。随邻里尺度的增加而增加，但当到达一定尺度后，变化趋于平缓，同样表明视域景观指数随邻里尺度的增加，对特征集聚的效应开始相对减弱。

2.2.3 不同邻里尺度的特征聚类

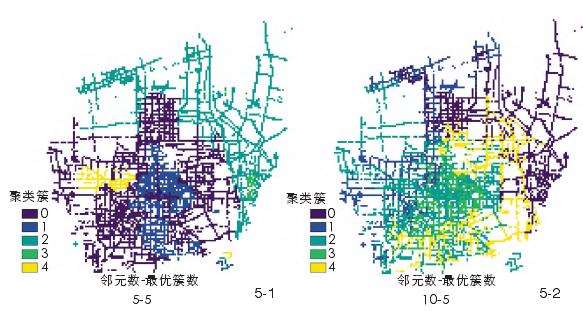
在邻元数不大于15时，分析所在采样点所考虑的邻近采样点数量较少，邻近采样点往往具有相似的特征组成和结构，并以GVI和SVF为聚类特征主导。因此，从聚类结果（图5）可以得知，当邻元数较小时聚类结果具有明显连续成片的分区特征。

例如当邻元数为5时，可以明显区分为西北区域、二环到绕城区间、老城（中心城区）和雁塔区、汉长安城未央宫区域，及灞桥区纺织城区域。当邻里尺度增加，KPSF（10，20]、KPSF（0，10]对特征聚类的影响开始增加，并超过SVF，分析所在采样点所考虑的邻近采样点数量较多，采样点之间的特征组成和结构变化增多，原来具有较大连续性集聚的特征分区，开始分解为较多分散的、小的集聚分区。对于特征的表述也从较小邻元数的局部性特征向较大邻元数的区域性特征转变。