成都供需平衡的公园绿地研究分4个步骤进行

四步研究法概述

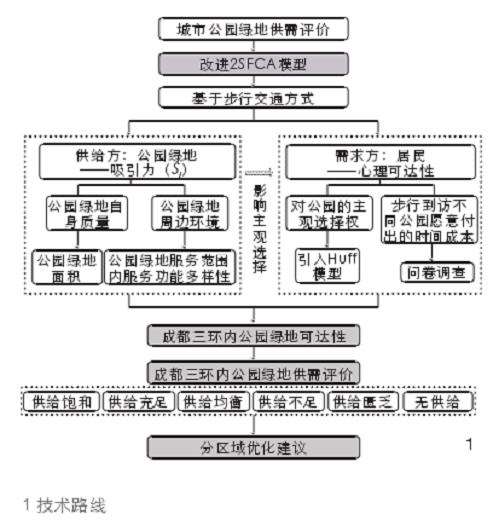
研究分4个步骤进行（图1）：

1）基于传统2SFCA模型，构建改进模型；

2）以成都市中心三环内城市公园绿地为例，利用改进前后的2SFCA模型分别计算其步行可达性，并进行量化对比分析；

3）利用公园绿地可达性进行供需分级评价；

4）结合公园绿地可达性，将供需进行分级，并提出针对性优化建议。

1.1 可达性模型改进：供给方与需求方优化

1.1.1 传统两步移动搜索法（2SFCA）

2SFCA模型最早是由JonhRadke提出，后有Luo和Wang进行两次搜索改进并命名为两步移动搜索法[15]。2SFCA模型计算可达性的原理是分别以公园绿地和居民点为中心进行两次搜索计算。传统2SFCA的计算如式（1）（2）所示：式中：i、k表示需求点；Rj为供需比；Sj为供给总和；dkj为供给方j与需求方k之间的服务成本；Dk为所有需求方（dkj≤d0）需求总和。dij为需求方i与j之间的服务成本；Ai为i的可达性，Ai数值越高则可达性越好。

1.1.2 基于改进2SFCA模型的可达性模型构建

基于传统2SFCA，本研究将从供需两方面进行改进。供给方考虑了公园绿地自身质量以及公园绿地周边环境对可达性的影响。

由于本研究对象较多，难以获取大量公园内部建设质量数据，因此只沿用了传统2SFCA中的公园面积，将其作为公园绿地自身质量的衡量因素。而描述公园周边环境选用了服务功能多样性，综合反映城市中人们的生活环境。需求方引入赫夫模型（Huff’smodel），考虑了居民因供给方吸引力不同、交通道路差异等客观因素，导致其主观选择到访不同公园的概率有所差别。

1）供给改善。作为城市公共服务空间，公园绿地会受到周边服务功能的影响，周边功能丰富度与公园到访率呈正相关[16]。同时本研究预调研显示，大部分居民（占比约65.9%）更愿意到访周边服务功能丰富的公园绿地，与文献研究结果一致。香农-维纳多样性指数（Shannon-Wienerdiversityindex）是一种能体现某区域内物种丰富度的指标，在当今研究中已经被衍生用于量化描述研究对象组成的多样性[17]。

兴趣点（pointofinterest,POI）是带有地理坐标、地址等信息的数据，其类型、数量以及密集程度可以有效地反映居民活动的空间分布状况[18]。因此本研究引入香农-维纳多样性指数公式，利用城市POI数据计算公园绿地服务范围内的服务功能（简称公园绿地周边服务功能）多样性Hj：式中：Hj为公园绿地j服务范围内的多样性；m为POI的类别数；i为某一类别的POI；Pji为公园绿地j服务范围内i类POI的数量占该类POI所在公园绿地服务范围内总POI数量的百分比。多样性指数值越大，说明公园绿地周边服务功能越多样。

将传统2SFCA模型与供给改善相结合，公园绿地j的综合吸引力Sj将由公园面积和公园绿地周边服务功能多样性2个因素决定：式中：γA和γj分别反映公园绿地面积（S′j）和公园绿地周边服务功能多样性（Hj）对公园绿地综合吸引力Sj的重要性，其中γA=γj=0.5。

2）需求改善。研究者Park发现，公园绿地的丰富度、公园绿地周边环境以及使用者对路程的心理容忍度是影响居民选择到访公园绿地的三大主要因素[19]。由此可知，公园绿地吸引力、公园绿地周边环境以及交通道路都会综合影响人们到访公园的主观选择，从而影响可达性。因此考虑居民对公园绿地主观选择的问题，本研究将引入Huff模型用以计算居民主观选择概率。

Huff模型是由美国DavidHuff教授提出的，用于客观计算某一服务设施的吸引力与研究区域内同类所有设施吸引力之和的比值[20]。目前Huff模型已被多次运用到公园绿地相关研究，如用于测算绿地实际吸引人口和服务半径[21]等。将Huff模型引入2SFCA模型中：式中：Pij为居民i基于Huff模型选择公园绿地j的概率；tij为i到j的时间成本；高斯函数（G）为时间距离摩擦力；Sj为j的吸引力，t0为时间阈值。

1.1.3 公园的空间可达性

1）结合公园绿地周边服务功能多样性和Huff模型，计算改进后的供需比：式中：Rj为公园绿地j的供需比；Sj为公园绿地j的综合吸引力；Pij为居民i选择公园绿地j的概率；Di为居民i的人口数量。

2）利用选择概率对供需比进行权重赋值，将加权后的进行求和，获得每个居民的可达性Ai：本研究改进的2SFCA模型，综合考虑了居民出行时间阻抗、选择概率以及公园绿地周边服务功能多样性对可达性的影响。

1.2 基于可达性的公园绿地供需分级评价

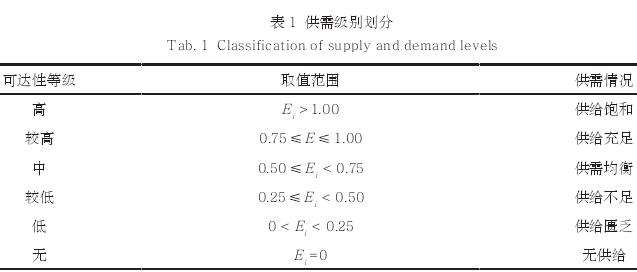
在公园绿地步行可达性结果基础上，利用式（9）进行供需衡量：式中Ei为空间公平性值，表示公园绿地和居民间的供需匹配关系。将计算结果划分为6个级别（表1）[22]，分别为供给饱和、供给充足、供需均衡、供给不足、供给匮乏、无供给。